Como saber a altura de um triângulo usando a área


A altura de um triângulo pode ser medida de diferentes maneiras, dependendo do tipo de triângulo e da informação que se tem ou se mede. Os triângulos retângulos, que incluem um ângulo de 90 graus, são os mais fáceis de medir usando o teorema de Pitágoras (se os comprimentos de dois lados forem conhecidos) ou a fórmula da área (se a área e a base forem conhecidas). Os triângulos equiláteros, em que todos os lados são de comprimento iguais, e os triângulos isósceles, em que três de seus lados são de comprimentos iguais, podem ser cortados ao meio, criando dois triângulos retângulos. Os triângulos oblíquos, os quais não têm o ângulo interior igual a 90 graus, são mais difíceis, e requerem a trigonometria para determinar a sua altura. A seguir, calcularemos a altura de um triângulo retângulo usando a fórmula da área.
Vai precisar de:
- Calculadora científica
- Transferidor
- Régua
Passos a seguir:
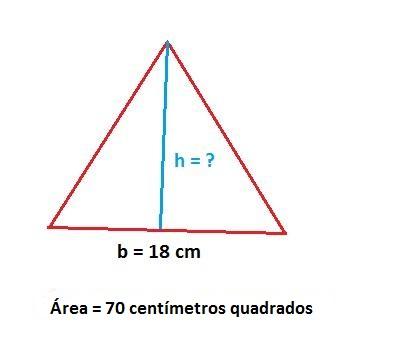
A primeira coisa a fazer para calcular a altura de um triângulo com área conhecida é desenhar o triângulo e escrever nos lados os valores conhecidos, como a área e os lados.
A seguir, escrever a fórmula da área de um triângulo, A = (1/2) · b · h, onde A = área b = base e h = altura.
Imaginemos que os valores que conhecemos são os que vemos na imagem.
Isolamos o h da equação para poder determinar o seu valor.
h = A / (0,5 b)

Ligue os valores conhecidos na equação anterior; obteremos o seguinte:
h = 72 / (0,5 x 18)
Faça cálculos para determinar a altura, portanto:
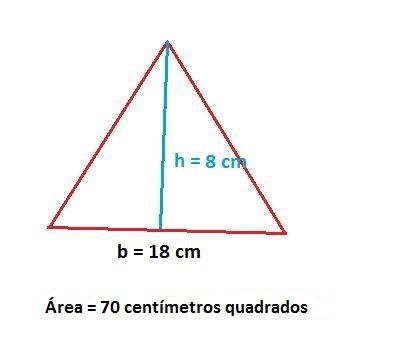
h = 72 / (0,5 x 18) = h = 72 / 9 = 8 cm
A altura do triângulo neste caso é de 8 cm.

Se pretende ler mais artigos parecidos a Como saber a altura de um triângulo usando a área, recomendamos que entre na nossa categoria de Formação.
Conselhos
- A base pode ser qualquer lado do triângulo.
- O método de trigonometria (utilizando seno) também pode ser aplicado a triângulos retângulos.
- Os três ângulos de um triângulo devem somar 180 graus.