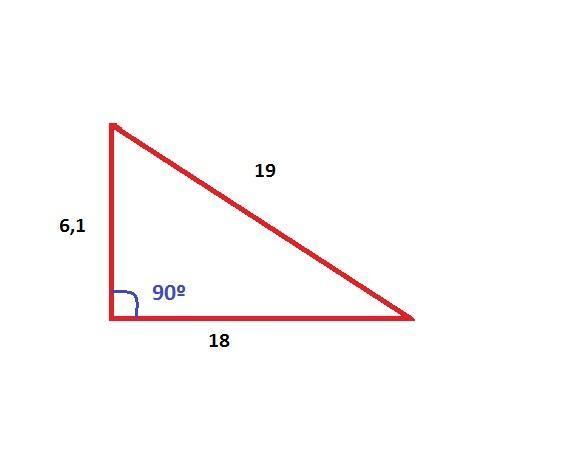
Como encontrar a altura de um triângulo retângulo usando o Teorema de Pitágoras


A altura de um triângulo pode ser encontrada de diferentes maneiras, dependendo do tipo de triângulo e da informação que se possui sobre suas medidas. Os triângulos retângulos que incluem um ângulo de 90 graus são os mais fáceis de medir usando o Teorema de Pitágoras (caso conheça a medida dos dois lados) ou a fórmula da área (caso conheça a medida da área e da base). Os triângulos equiláteros, onde todos os lados possuem a mesma medida, e os triângulos isósceles, onde três dos seus lados são iguais, podem ser cortados a meio, criando dois triângulos retângulos. Os triângulos oblíquos são aqueles que não têm o ângulo interior de 90 graus e são mais difíceis pois requerem a trigonometria para encontrar sua altura. De seguida, em umComo.com.br mostramos-lhe como encontrar a altura de um triângulo retângulo usando o Teorema de Pitágoras.
Vai precisar de:
- Calculadora científica.
- Transferidor.
- Régua.
Passos a seguir:
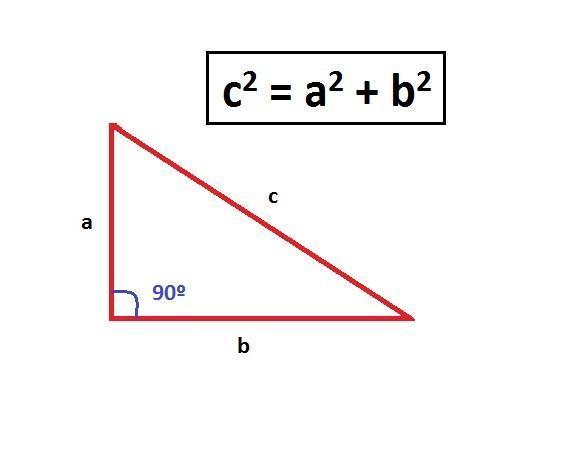
O primeiro que você deve fazer para calcular a altura de um triangulo é escrever o Teorema de Pitágoras, c^2 = a^2 b^2, onde c é a hipotenusa (a diagonal).

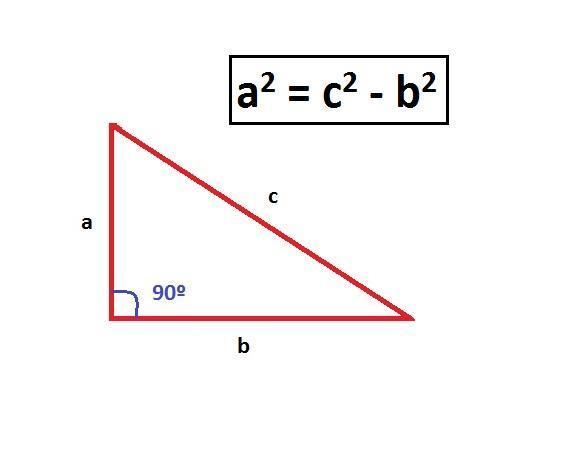
Reorganize o Teorema para resolver a^ 2, portanto a ^ 2 = c ^ 2 - b ^ 2 Queremos encontrar o valor de "a" pois como vemos na imagem, "a" corresponde à altura do triângulo.

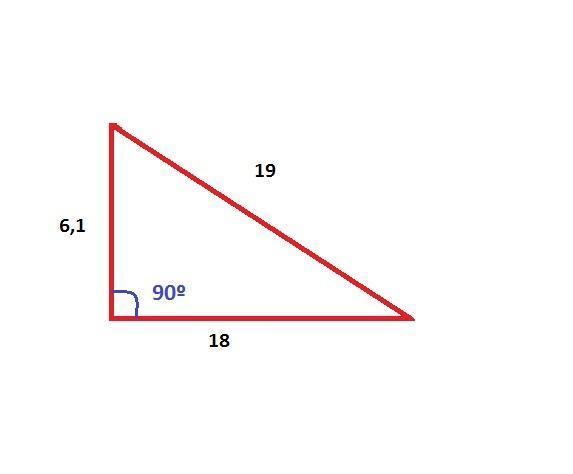
Conecte os dois lados de valores conhecidos "c" e "b", que no nosso caso possuem o valor de:
- c = 19
- b = 18
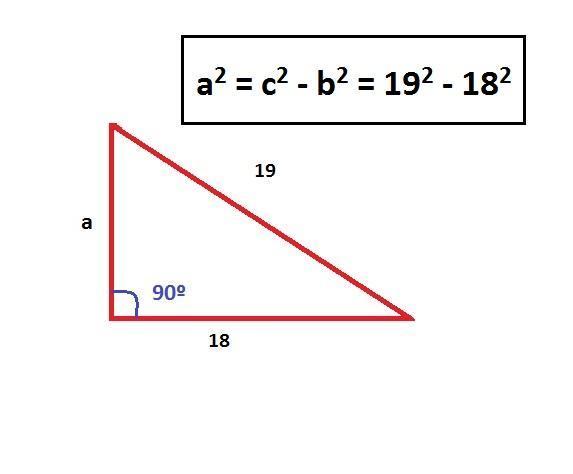
Portanto temos [a ^ 2 = 19 ^ 2 - 18 ^ 2]
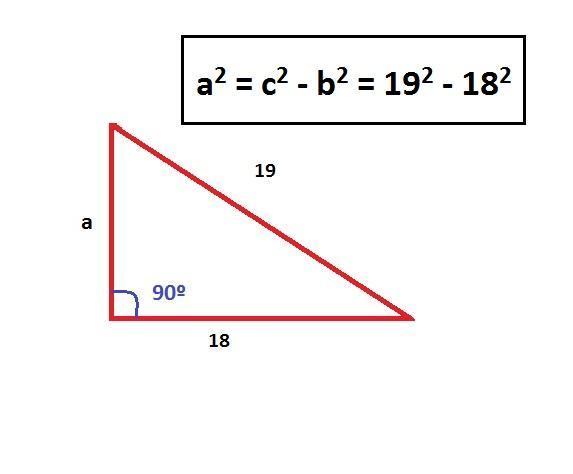
A seguir, resolvemos a equação e temos o seguinte:
a ^ 2 = 361 - 324 = 37
Para terminar e encontrar o valor real da altura do triângulo, você deve saber a raiz quadrada de ambos os lados para encontrar a altura a^ 2. [a = 6.1]

Se pretende ler mais artigos parecidos a Como encontrar a altura de um triângulo retângulo usando o Teorema de Pitágoras, recomendamos que entre na nossa categoria de Formação.
Conselhos
- A base pode ser qualquer lado do triângulo.
- O método da trigonometria (usando o seno) também pode ser aplicado em triângulos retângulos.
- Os três ângulos de um triângulo devem somar 180 graus.