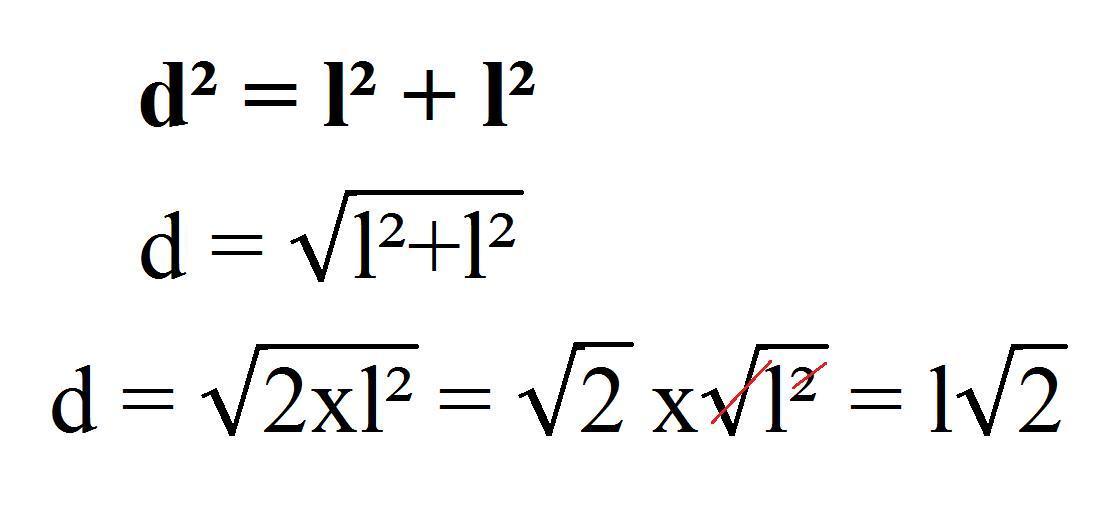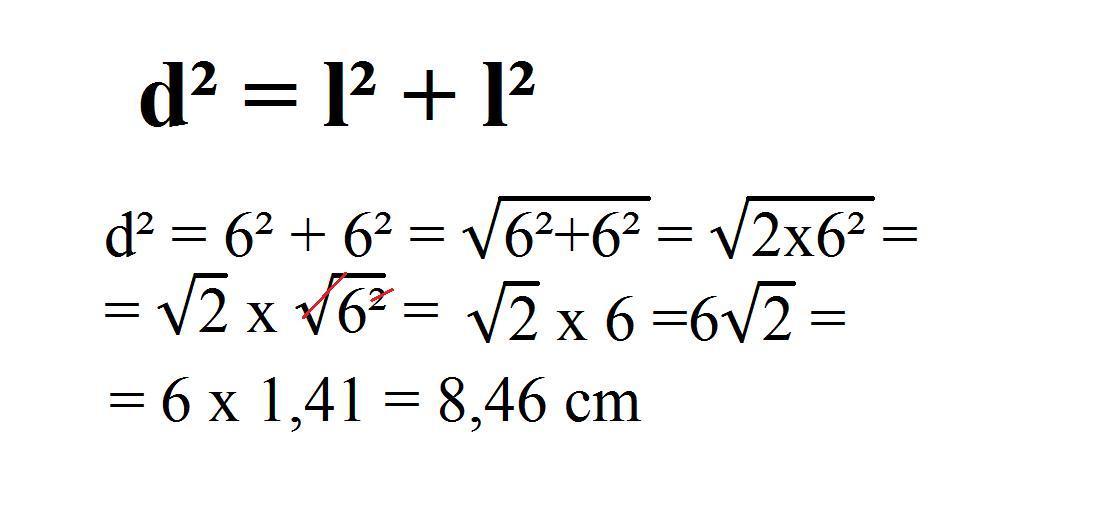Como calcular a diagonal de um quadrado

Encontrar a diagonal de um quadrado é uma operação simples e bastante necessária quando aprendemos geometria básica, de forma que o conceito poderá ser aplicado em diversos contextos e nos ajudar até mesmo em exercícios mais complexos que exigem um pouco mais do nosso raciocínio. Para encontrar o valor, existe uma fórmula que pode ser aplicada e que tornará obtenção bastante simples. Também é válido dizer que, já que todos os quadrados têm duas diagonais do mesmo comprimento, você conseguirá achar o valor de uma delas, conseguirá saber o valor da outra, sendo desnecessário fazer mais cálculos.
Está procurando a fórmula para achar a diagonal de um quadrado? Neste artigo do explicamos umCOMO como calcular a diagonal de um quadrado.
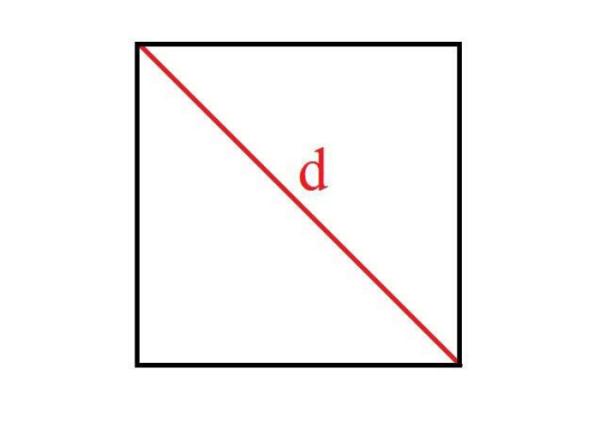
Diagonal do quadrado
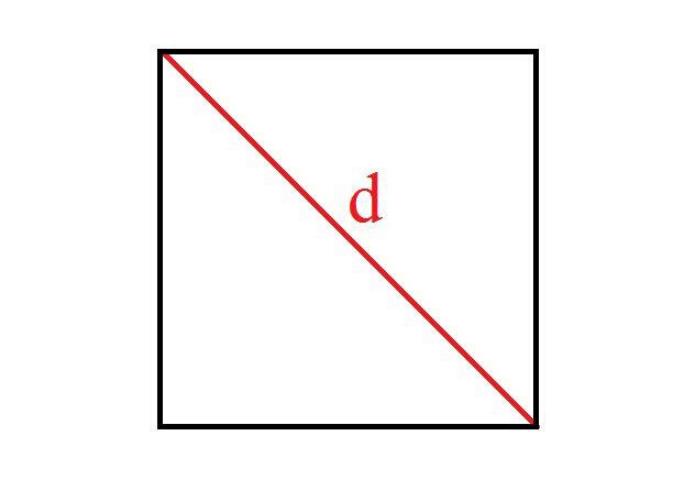
Em primeiro lugar, será necessário que antes de aprender a calcular a diagonal de um quadrado entenda o que é uma diagonal. A diagonal é uma linha que une dois vértices que não sejam consecutivos e que pode ser encontrada em qualquer polígono. Já quadrados têm apenas 4 vértices, conseguimos encontrar apenas 2 diagonais que unem seus vértices opostos.
É possível encontrar os vértices e suas medidas em todos os polígonos e todos terão o mesmo tamanho, sendo assim, ao calcular uma diagonal de um quadrado, obteremos também o valor da outra.
Como calcular a diagonal de um quadrado
Para encontrarmos o valor em questão, devemos aplicar a fórmula da diagonal do quadrado, segundo a qual o quadrado da diagonal de um quadrado é igual à soma do quadrado dos seus lados. Assim sendo, será necessário desenvolver a fórmula para conseguir o valor da diagonal, o que é bastante simples e será explicado abaixo caso você não se lembre bem como realizar a operação. A fórmula da diagonal do quadrado é a seguinte.
- d² = l² + l²
Em matemática, quando colocamos um ² logo após um valor, significa que devemos multiplicá-lo por ele mesmo, sendo assim, a fórmula por extenso é:
- d.d = l.l + l.l
Deste modo, devemos recordar que a operação oposta ao quadrado é a raiz quadrada, de tal forma que a diagonal será igual à raiz quadrada da soma do quadrado dos lados, que é o mesmo que a raiz do dobro do lado ao quadrado.
Como os elementos dentro d raiz se multiplicando entre si, podemos separá-los em duas raízes de tal forma que a diagonal do quadrado será igual à raiz de dois multiplicada pela raiz do lado ao quadrado e, nesse momento, podemos anular a raiz e o quadrado e obter finalmente a fórmula segundo a qual a diagonal é igual ao comprimento do lado do quadrado multiplicado pela raiz quadrada de dois:
- d = l√2

Diagonal do quadrado: fórmula aplicada
Para que possamos entender de forma mais clara, vejamos um exemplo prático onde aplicamos a fórmula, assim sendo, suponhamos que temos um quadrado cujo lado mede 6 cm:
- d² = l² + l²
- d² = 6² + 6²
Se desenvolvermos a fórmula, chegamos a:
- d = 6√2
Observe acima que, em um quadrado com lado 6, a diagonal será o valor de seu lado multiplicado por √2, ou seja, 6√2. A fórmula assim simplificada por ser utilizada em qualquer quadrado, entretanto, é recomendável que inicialmente façamos o cálculo completo para memorizarmos os mecanismos que estão por trás da simplificação.
E ao realizar a operação matemática obtemos que o comprimento da diagonal de um quadrado de 6 cm de lado é de 8,46 cm.
Dica: caso você esteja fazendo exercícios de matemática de múltipla escolha, é muito possível que a resposta final não seja completamente desenvolvida e que você encontre "6√2" como resultado. Por via das dúvidas, cheque antes de fazer as contas para não perder tempo calculando algo que será desnecessário.
Se você ainda estiver com dúvidas, veja na imagem abaixo o desenvolvimento minucioso do cálculo e veja também como fazer uma raiz quadrada.
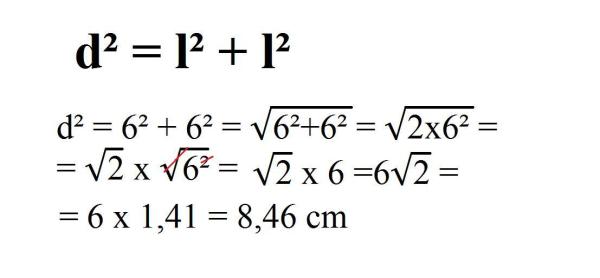
Origem da fórmula da diagonal do quadrado
Além de aprender como utilizar a fórmula para encontra a diagonal de um quadrado, também é válido aprender de onde a fórmula surgiu, afinal, houve um raciocínio por trás que pode ser utilizado em diversos outros contextos e exercícios. A fórmula em questão veio do conhecido Teorema de Pitágoras, que estipula uma relação entre a hipotenusa e os catetos de um triângulo retângulo. Tal teorema data do século VI a.C. e envolve algumas definições que devem ser conhecidas antes de aplicá-lo. Vamos então às definições dos termos necessários:
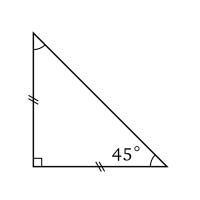
- Triângulo retângulo: qualquer triângulo que tenha um dos ângulos internos com 90º, ou seja, um ângulo reto.
- Cateto: menores lados de um triângulo e que, em um triângulo retângulo, irão compor o ângulo reto em seu encontro.
- Hipotenusa: maior lado de um triângulo.
Visto que um quadrado tem 4 ângulos de 90º, quanto o cortamos diagonalmente, acabamos com um triângulo retângulo, como pode ter observado na imagem abaixo. Em razão dessa propriedade da figura geométrica, podemos utilizar o Teorema de Pitágoras para encontrar a diagonal de um quadrado.

Exercício para calcular a diagonal de um quadrado
Para fixar bem o cálculo de diagonal do quadrado, nada melhor do que fazer exercícios. Se você está estudando para provas ou para o vestibular, será fácil encontrar exercícios do tipo em seu material, entretanto, veja também abaixo um exercício que irá te ajudar a fixar a matéria:
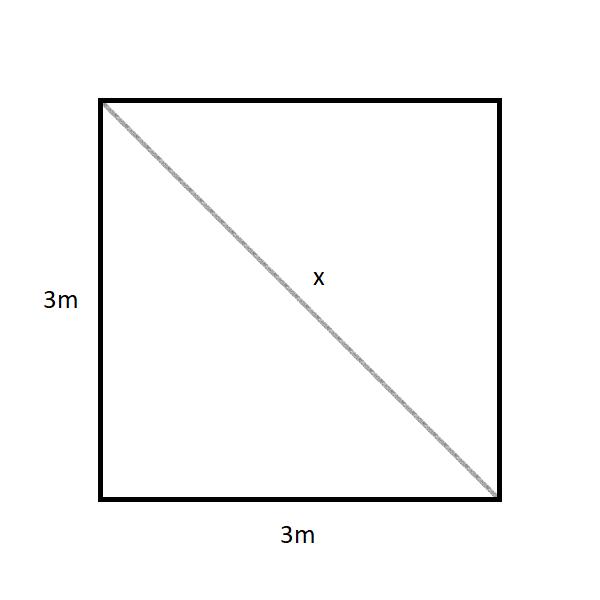
- José irá planificar uma área transformá-la em uma rampa que será utilizada para o transporte de materiais fornecidos por sua loja. Apesar de ser uma tarefa simples, José precisa saber qual será a extensão da rampa visando adquirir azulejos suficientes para a cobertura da área. Considerando que a altura da rampa e que sua extensão horizontal são ambas de 3 metros, qual será a extensão da rampa?
Veja abaixo uma imagem que simula a área a ser analisada para ajudar a visualizar a situação.
Resposta: Como pode ser visualizado abaixo, a extensão da rampa será a hipotenusa de um quadrado com 3 metros em cada um dos seus lados. Para encontrar o número procurado, devemos então considerar a rampa como a diagonal de um quadrado e aplicar a fórmula.
- d² = l² + l²
- d² = 3² + 3²
Se desenvolvermos a fórmula, chegamos ao seguinte resultado:
- d = 3√2 = 4,23m
Em alguns exercícios mais complexos de geometria, nos deparamos com cálculos que nos exigem um pouco mais do que apenas o Teorema de Pitágoras. Se quer fazer outros cálculos de figuras geométricas e precisa de ajuda, não deixe de consultar estes artigo:
- Como encontrar o perímetro de um quadrilátero
- Como encontrar o volume de um cubo
- Como calcular o perímetro de uma circunferência

Se pretende ler mais artigos parecidos a Como calcular a diagonal de um quadrado, recomendamos que entre na nossa categoria de Formação.