Diferença entre média e mediana


Às vezes é difícil decidir qual é o melhor agregador, especialmente quando se refere à média e à mediana. Você sempre tem a opção de usar os dois, ou seja, uma métrica para o cálculo da média e outra para o cálculo da mediana. Isso permitirá que você verifique qual é a métrica mais útil para cada caso específico. Mesmo assim, o entendimento dos dois termos estatísticos será de grande ajuda para tomar a decisão certa mais rapidamente.
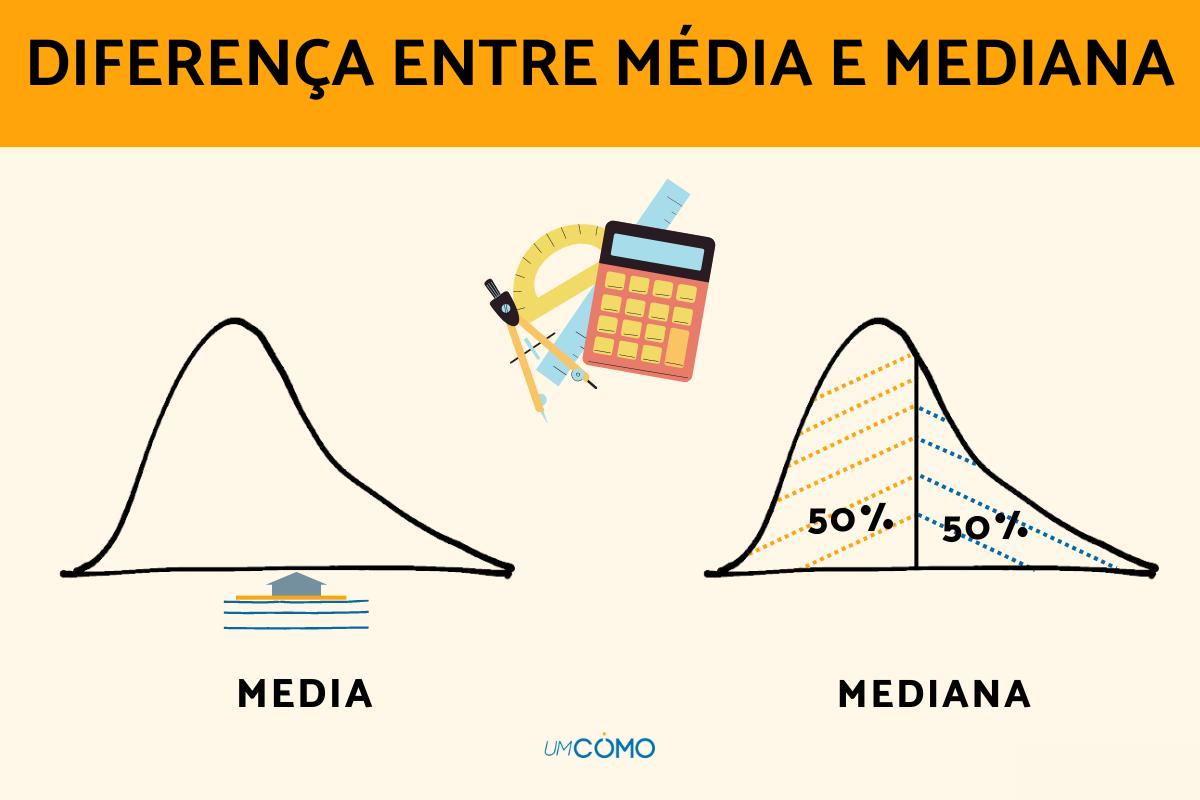
A média e a mediana têm funções semelhantes no entendimento da tendência central de um grupo ou conjunto de números. No entanto, é importante saber o que significa cada termo para não confundir a nível estatístico e, dessa maneira, usá-los no momento mais apropriado. Para descobrir a diferença entre média e mediana, como elas são calculadas e exemplos de ambos os conceitos, no umCOMO recomendamos que você continue lendo este artigo.
Como calcular média aritmética
A média, conhecida como média aritmética em relação ao campo estatístico para se distinguir de outros meios, como geométrico, quadrático ou harmônico, pode ser definido como o valor médio ou a média de um conjunto de dados.
Esse valor médio do conjunto de números pode ser calculado adicionando todos os valores do conjunto de dados e, posteriormente, dividindo pelo número de valores que esse conjunto contém.
A média aritmética é usada em matemática, estatística e economia com frequência. Além disso, também é usada em antropologia, história e, até certo ponto, na maioria dos campos acadêmicos. Sem mais, o cálculo da renda per capita de cada país é a renda aritmética média de sua população.
Embora a média aritmética seja frequentemente usada para relatar tendências centrais, não é uma estatística robusta porque tem uma grande influência dos valores atípicos (valores muito mais altos ou mais baixos que a maioria dos outros).
Quanto às distribuições assimétricas, como é o caso da distribuição da renda, na qual a renda de um pequeno grupo de pessoas é muito superior às da grande maioria, a média aritmética talvez não coincida com a noção de "médio". Nesses casos, existem estatísticas robustas que podem ser usadas como mediana, que fornece uma descrição mais adequada da tendência central.
Como calcular mediana
O termo mediana vem do latim medianus e pode ser traduzido como "o meio". Essa definição facilita muito o conceito. Como a estatística mediana é precisamente isso, o número localizado logo no meio de um conjunto de valores ou dados ordenados de mais baixo a mais alto ou inverso, ou seja, do mais alto para o mais baixo.
Quando você tem um conjunto de dados que é par, não pode haver valor central. Nesse caso, para obter a mediana, você precisa calcular a média aritmética correspondente aos dois valores centrais desse conjunto.
Sendo simples de entender e calcular, além de ser uma abordagem robusta da média, a mediana é uma estatística de resumo popular nas estatísticas descritivas. Nesse contexto, existem diferentes opções para uma medida de variabilidade, como intervalo, intervalo interquartico, desvio médio e desvio absoluto médio.
Na prática, as diferentes medidas de localização e dispersão são geralmente comparadas de acordo com o quão bem os valores da população extraídos de uma amostra de dados podem ser estimados. Nesse sentido, a mediana é estimada a partir da amostra mediana e possui boas propriedades.
Embora geralmente não seja ideal se estiver sujeita a uma distribuição populacional específica, suas propriedades são sempre razoavelmente boas.

Quais são as diferenças entre média e mediana
É importante que você entenda a diferença entre média e mediana, tanto na aritmética quanto no ponto de vista da teoria matemática, estatística e de probabilidade. A principal diferença entre os dois termos é que a média é o valor médio correspondente a um conjunto de números, enquanto a mediana se refere ao ponto médio ou ao valor central de um conjunto de números, que são mostrados começando pelo menor valor e terminando para o valor mais alto.
Outra diferença entre a média e a mediana é que a primeira não é uma ferramenta robusta a ser muito influenciada por certos valores atípicos. Por outro lado, a mediana é mais apropriada para derivar as distribuições tendenciosas para a tendência central, porque é mais robusta e sensível.
Exemplos de média e mediana
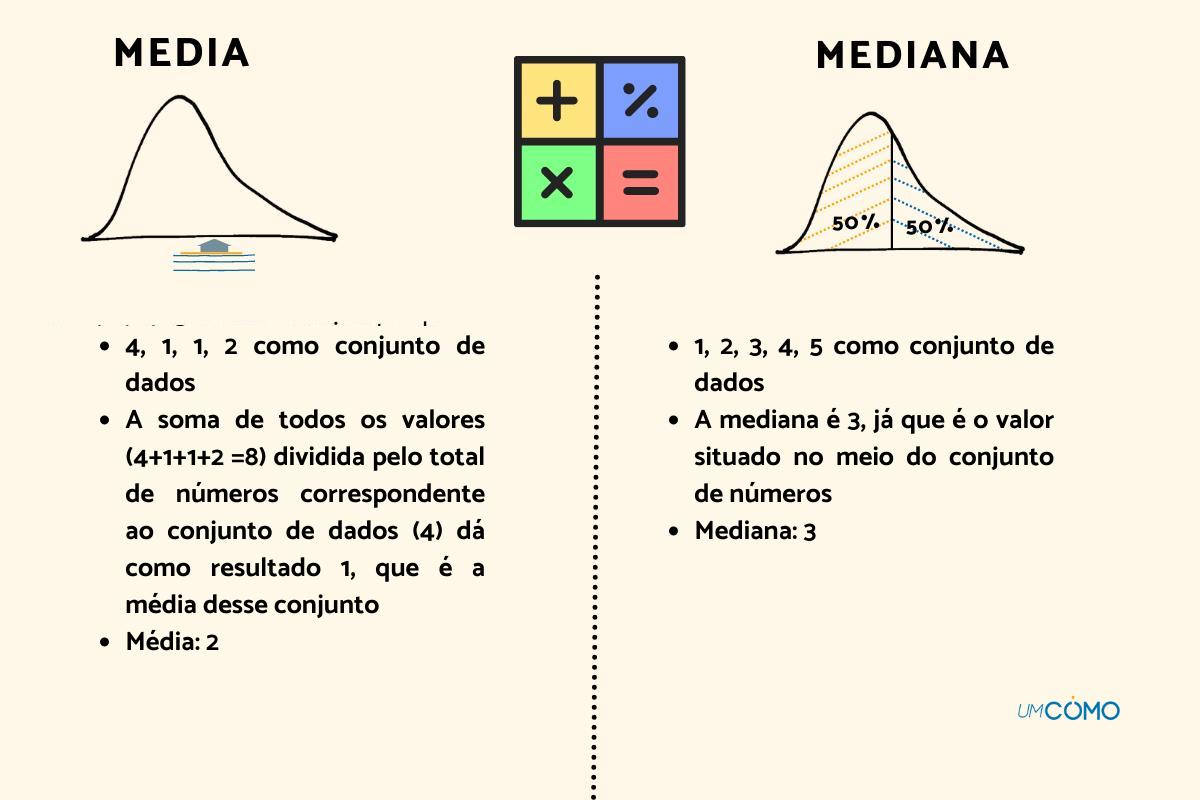
- Média: 4, 1, 1, 2 como um conjunto de dados. A soma de todos os valores (4+1+1+2 = 8) dividida pelo número total correspondente ao conjunto de dados (4) resulta em 2, que é a média desse conjunto.
- Mediana: 1, 2, 3, 4, 5 como um conjunto de dados. A mediana é 3, pois é o valor localizado no meio do conjunto de números.
Agora que você sabe a diferença entre média e mediana, como elas são calculadas e exemplos de ambos os conceitos, te ensinamos tudo sobre o Máximo Divisor Comum: o que é e como encontrá-lo e o Mínimo Múltiplo Comum: o que é e como encontrá-lo.

Se pretende ler mais artigos parecidos a Diferença entre média e mediana, recomendamos que entre na nossa categoria de Formação.